Research Article - (2022) Volume 13, Issue 1
COVID-19 Data Published by Turkey is Fake or Not?
Hasraddin Guliyev*Abstract
Turkey attempt to control the fast-rising number of coronavirus cases and deaths since the spread of coronavirus disease 2019 (COVID-19) in every country. Likewise, researchers from different fields have been an effort to explore COVID-19 with distinctive aspects for minimizing the cost of a pandemic on the economy and social life. We know that is impossible reliable and unbiased results of studies without accurate data. Thus, if we gather inadequate data and analysis it, we will be faulty decisions and make policies. For this reason, Benford's Law may be useful for assessing the effects of the current control interventions and may be able to answer the question, ‘‘How flat is flat enough?’’. In this study, we explore whether the COVID-19 data published by Turkey is fake or not with Benford's Law.
Keywords
Benford’s law, COVID-19, Data quality
Introduction
On December 31, 2019, twenty-seven cases of pneumonia with no known cause were discovered in Wuhan, Hubei Province, China. With over 11 million inhabitants, Wuhan is the most densely populated city in central China. The bulk of the affected positions were admitted to hospitals with fever, dyspnea, dry cough, and bilateral lung infiltrates as seen on imaging in the 27 cases. All the incidents were connected to the Huanan Seafood Wholesale Market in the area, which primarily sells a variety of fish as well as live animals like marmots, bats, chickens, and snakes (Lu R, et al., 2020). On January 7, 2020, the causative agent was discovered in throat swab samples taken by the Chinese Centre for Disease Control and Prevention (CCDC). The World Health Organization (WHO) announced the coronavirus disease 2019 (COVID-19) to be the cause of Serious Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) (WHO 2020).
To date, most patients with SARS-CoV-2 have had developed mild symptoms, such as sore throat, dry cough, and fever. Many cases have been unexpectedly determined. However, a minority of patients have been known to develop fatal complications, such as septic shock, organ failure, severe pneumonia, pulmonary oedema, and acute respiratory distress syndrome. As per recent statistics, 54.3% of those diagnosed with SARS-CoV-2 were male with a median age of 56 years. Patients who required intensive care help were, on average, older and/or were previously diagnosed with comorbidities, such as cerebrovascular, cardiovascular, digestive, endocrine, and chronic respiratory disease. Those in intensive care were also more likely to report abdominal pain, dizziness, dyspnoea, and anorexia (Ruan Q, et al., 2020).
Globally, 28 February 2021, there have been 113.472.187 confirmed cases of COVID-19, including 2.520.653 deaths, reported to WHO (WHO, 2021). As of February 28, 2021, there have been 2.701.588 total confirmed cases of COVID-19, including 28 569 deaths and, 3.317.516 diagnostic tests for COVID-19 (TR Ministry of Health, 2021).
Since COVID-19 became the most serious public health issue in many countries, the challenges of performing cross-country comparisons were raised. Comparing COVID19 statistics across countries presents several challenges. For example, developing reliable tests and criteria for diagnosing COVID19 in the early stages of the disease takes time; many countries have different diagnostic criteria; determining the cause of death of patients who show little of the known COVID-19 symptoms is difficult, and the leaders of some countries do not provide much transparency in the flow of information on the disease. Data sharing practices at the early stages of the pandemic were inadequate and led to policy errors in Turkey as some country. Contrary to popular speculation, we use a statistical fraud detection technique, Benford’s Law (Benford F, 1938), to assess the veracity of the statistics in Turkey. We believe these findings are significant because COVID-19 had a greater impact on Turkey, and some researchers may have gotten biased empirical results because of using inaccurate COVID-19 data. Furthermore, continuing doubts about the validity of the released statistics are worrying because they influence policy decisions made by countries that have seen epidemics later. Data sharing practices at the early stages of the pandemic were inadequate and led to policy errors in Turkey as some country. Contrary to popular speculation, we use a statistical fraud detection technique, Benford’s Law (Varian HR, 1972), to assess the veracity of the statistics in Turkey. These findings are important because Turkey was more affected from COVID-19 and some researchers by now get to biased empirical result due to use inaccurate COVID-19 data. In addition, the on-going doubts over the credibility of its published data are problematic as it impacts subsequent policy choices by countries that saw epidemics later.
Methodology
Based on the distribution of the first digits of observed data, Benford's Law is used to detect fraud or flaws in data collection. In a forensic study looking for possible manipulations of the number of cases (Maximilano MZ, et al., 2019), testing for the validity of Benford's Law in this dataset will be the best method, since a distribution of first digits that deviates from the predicted distribution could indicate fraud. For exponential processes with multiple magnitude changes, a Benford distribution of first digits emerges naturally (Michalski T and Stoltz G, 2013). Benford's Law has been used to detect economic statistics manipulation by Nye and Moul (Nye J and Moul C, 2007; Garcia GJ and Pastor G, 2009; Rauch B, et al., 2011; Holz CA, 2014). Recent advances in statistics and economics have expanded Benford's Law beyond the natural environment to detect fraud in social activities such as accounting (Nigrini MJ, 2015), international trade (Barabesi L, et al., 2018) and elections (Pericchi L and Torres D, 2011; Deckert J, et al., 2011). Based on the distribution of the first digits of observed data, Benford's Law is used to detect fraud or flaws in data collection. For exponential processes with multiple magnitude changes, a Benford distribution of first digits emerges naturally (Michalski T and Stoltz G, 2013). Benford's Law has been used to detect economic statistics manipulation by Nye and Moul, Garcia and Pastor, Rauch, Holz and Nigrini (Nye J and Moul C, 2007; Garcia GJ and Pastor G, 2009; Rauch B, et al., 2011; Holz CA, 2014; Nigrini MJ, 2015). Recent advances in statistics and econometrics have expanded Benford's Law beyond the natural environment to detect fraud in social activities such as accounting (Nigrini MJ 2015), stock prices, international trade (Barabesi L, et al., 2018) and elections (Pericchi L and Torres D, 2011; Deckert J, et al., 2011). Alali used financial accounting data to see if there are any anomalies from Benford's Law on publicly accessible data in the United States for the decade beginning in 2001 (Alali FA and Romero S, 2013). The degree of manipulation was influenced by the effectiveness of legislation, increased scrutiny, and being audited by Big 4 firms. Researchers conducted a parallel analysis on European publicly traded firms, in which they analysed the accuracy of selected accounting items such as net profit, equity, revenue, total assets, and profitability ratios created by these items with Benford's Rule. The accounting item distribution was found to be consistent with the theoretical distribution predicted by the statute. In the case of financial ratios, there was a deviation from the rule, but it was at an appropriate standard in the case of return on revenue and return on equity. Benford's Law has also been used to assess the accuracy of government-released macroeconomic results. As a result, the used data on the public deficit, public debt, and gross national product derived from the Eurostat database for 27 EU member states for the years 1999 to 2009 (Rauch B, et al., 2014). Greece, Romania, Latvia, and Belgium had the most data deviated from Benford's Law in terms of the first digit, according to the findings. However, it must be emphasized that deviation should not be interpreted as a clear indication of manipulation; rather, it implies that non-conformities should be investigated further. Researchers conducted another analysis to see whether international macroeconomic figures complied with Benford's Law (Nye J and Moul C, 2007). Analyses were conducted on a dataset of 183 countries, with a subset of OECD countries being examined in greater depth. Overall, the findings showed that, while data from OECD countries complied with the law, developed country GDP figures had some inconsistencies.
Discussion
Benford’s law
Benford's Law was an empirically discovered pattern in many real-life datasets for the frequency distribution of first digits (Boyau JR, et al., 2015). It notes that the leading digit is nonuniformly distributed in a consistent manner in many naturally occurring sets of numbers. Furthermore, the leading significant digit will most likely be tiny. For instance, 1 appears as the first digit 30.1 percent of the time, while 9 appears as the first digit 4.5 percent of the time. The number 1 appears more than six times more often than the number 9 in this case.
On a logarithmic scale, the probability of occurrence of digit d is proportional to the space between d and d+1, according to equation (1). In other words, on the logarithmic scale, the likelihood of two consecutive digits occurring is equal. The odds for the first digits are as follows;
(d1)=log10(1+1d1) For all d1(1,2,......,9) (1)
Furthermore, the first two digits probabilities can be denoted as;
(d1d2)=log10(1+1d1d2) For all 1d1d2∈(11,12,.......,99) (2)
Where d1 and d2 denotes the first and the first two digits significant.
From a statistical standpoint, a Borel probability measure P on R is Benford if p({χ ∈R : S (χ ) ≤ u}) = logu for all u∈[1,10) , where S is the significant of a real number is its coefficient when it is expressed as a floating point. That is, the significant function S : R→[1,10) is defined as follows: if x is a non-zero real number, then S (χ ) = u , where u is the unique number in [1,10) with |x|=10κu for some κ∈z. Then, a random variable X is Benford if its distribution PX on R is Benford, i.e., if pχ ({χ ∈R : S (χ ) ≤ u}) = log u for all u∈[1,10) .
The useful result for this study is that if U is a random variable uniformly distributed on [0, 1), then the random variable X=10U is Benford. To show this, let us say the cumulative distribution function of a Benford random variable X is FX (x)=log10 (x) for all x ∈ [1, 10). Thus, a Benford variable X can be generated by 10U, where U ˜ U (0, 1).
The Pearson's Chi-squared Goodness-of-Fit Test was used to assess the deviation between the observed and predicted first digit distribution from Benford's Law (Pearson KFRS, 1900). The statistic for the corresponding 2 can be calculated as;
χ stat2 =Σ(Oi − pi)2 pi9i = 0
where Oi is the observed frequency in each bin in the observed data, and Pi is the expected frequency based on Benford’s distribution. In addition, we test a goodness-of-fit between observed frequency and expected frequency with Kolmogorov- Smirnov D statistic (Kolmogorov A, 1933), Chebyshev distance m statistic (Drew JH, 2000), Euclidean distance d statistic (Cho WKT, Gaines BJ, 2007), Judge-Schechter mean deviation statistic (Judge G and Schechter L, 2009) Shapiro-Francia type correlation test Joenssen’s JP2 statistic (Shapiro SS and Francia RS, 1972) and Joint Digit Test T2 statistic.
The test statistic works as a measure of the gap between the realization observed in the data and that implied by the Benford distribution (Joenssen DW and Muellerleile T, 2015); the larger the test statistic is, the stronger the deviation from the Benford distribution will be. Then, the null hypothesis (H0) is that the observed distribution of the first significant digit in the case of interest is the same as expected based on Benford distribution; the alternative hypothesis (Ha) is that the observed distribution of the first significant digit in the case of interest is not the same as expected based on Bedford distribution. Particularly in analysis, if the null hypothesis can be rejected, the observed series does not satisfy Benford distribution and thus infers a possible manipulation of data or published data is fake.
Empirical results
The Johns Hopkins University Corona Virus Research Center provides us with regular confirmed COVID-19 case data for Turkey. Our dataset contains 350 observations between the dates of March 16, 2020, and February 28, 2021. Since the COVID-19 pandemic is in its exponential growth phase, we use the growth rate of reported cases for Benford`s Law research.
Table 1 and Figure 1 represent the growth of reported cases, first digit frequency and distribution, Benford's Law frequency and distribution, and the discrepancy between first digit frequency (observed frequency) and Benford frequency (expected frequency).Chi-Square test (p-value=0.021), Hotelling T-square test (p-value=0.041), Joenssen’s JP-square test (p-value=0.026), Kolmogorov-Smirnov (K-S) test (p-value=0.036) and Judge- Schechter Normed Deviation test (p-value=0.033) do not reject the null hypothesis at the 1% level and support a Benford distribution. Furthermore, the Euclidean Distance test (p-value=0.062) and the Chebyshev Distance test (p-value=0.074) do not reject the null hypothesis at the 5% level, so the observed distribution of the first digit is the same as Bedford distribution at the sample period.
| Digits | Digits frequency | Digits distribution | Benford frequency | Benford distribution | Difference of frequency |
|---|---|---|---|---|---|
| 1 | 109 | 31.14% | 105.36 | 30.10% | 3.64 |
| 2 | 52 | 14.86% | 61.632 | 17.61% | -9.632 |
| 3 | 27 | 7.71% | 43.729 | 12.49% | -16.729 |
| 4 | 36 | 10.29% | 33.919 | 9.69% | 2.081 |
| 5 | 29 | 8.29% | 27.713 | 7.92% | 1.287 |
| 6 | 23 | 6.57% | 23.431 | 6.70% | -0.431 |
| 7 | 28 | 8.00% | 20.297 | 5.80% | 7.703 |
| 8 | 29 | 8.29% | 17.903 | 5.12% | 11.097 |
| 9 | 17 | 4.86% | 16.015 | 4.58% | 0.985 |
Chi-Squared test, ᵪ2=18.088 p-value=0.021
Euclidean distance test, d=1.2823 p-value=0.062
Hotelling T-square test , Hotelling T2=8.2563 p-value=0.041
Joenssen’s JP-square test, JP-square=0.91379 p-value=0.026
Kolmogorov-Smirnov (K-S) test, D=1.215 p-value=0.036
Chebyshev distance (maximum norm) test, m=0.89418 p-value=0.074
Judge-Schechter normed deviation test, a* =0.050319, p-value=0.033
Table 1: First digits distribution the growth of confirmed case and tests of significance
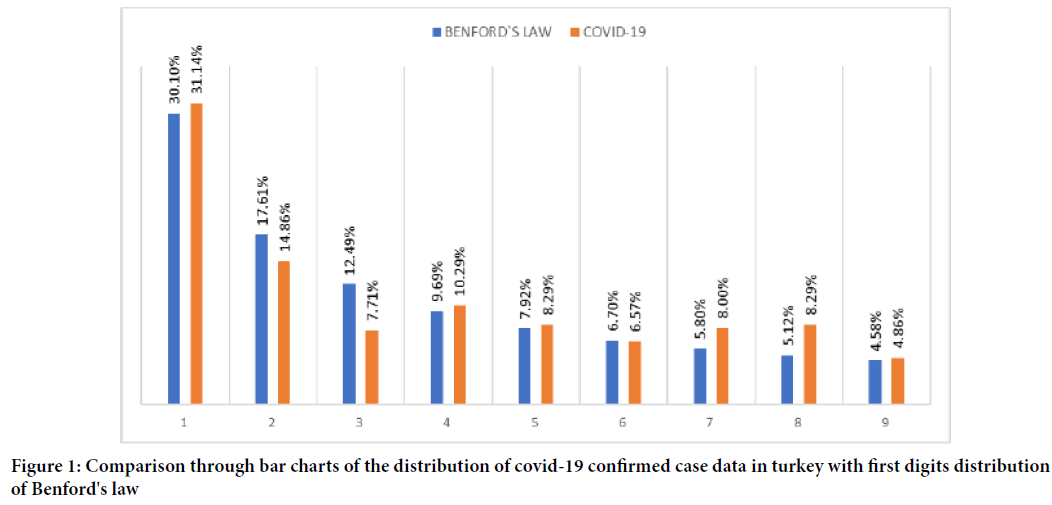
Figure 1: Comparison through bar charts of the distribution of covid-19 confirmed case data in turkey with first digits distribution of Benford's law
Most of the prior studies in the field of Benford’s Law have focused on first or second digits. However, the joint analysis of the first two digits may also disclose anomalies that would be missed with the sole analysis of the first or second digits (Nigrini MJ, 2007). In this respect, the observed frequencies of the first two digits are calculated against the expected frequencies of Benford’s Law (Table 2). Table 2 and Appendix A produce the growth of confirmed cases frequency and distribution of the first two digits, the frequency and distribution of Benford’s Law, the difference of the first two digit`s frequency (observed frequency) and Benford frequency (expected frequency). Chi-Square test (p-value=0.299), Euclidean Distance test (p-value=0.484), Hotelling T-square test (p-value=0.659), Joenssen’s JP-square test (p-value=0.337), Kolmogorov-Smirnov (K-S) test (p-value=0.163) and Judge- Schechter Normed Deviation test (p-value=0.847), do not reject the null hypothesis at 1%, 5% and 10% levels and is that the observed distribution of the second significant digit in the case of Turkey is the same as expected based on Benford distribution.
| Digits | Digits frequency | Digits distribution | Benford frequency | Benford distribution | Difference of frequency |
|---|---|---|---|---|---|
| 10 | 10 | 2.86% | 1448.70% | 4.14% | -448.70% |
| 11 | 18 | 5.14% | 1322.60% | 3.78% | 477.40% |
| 12 | 14 | 4.00% | 1216.70% | 3.48% | 183.30% |
| 13 | 15 | 4.29% | 1126.50% | 3.22% | 373.50% |
| 14 | 13 | 3.71% | 1048.70% | 3.00% | 251.30% |
| 15 | 12 | 3.43% | 9.81 | 2.80% | 2.19 |
| 16 | 8 | 2.29% | 9.215 | 2.63% | -1.215 |
| 17 | 11 | 3.14% | 8.688 | 2.48% | 2.312 |
| 18 | 5 | 1.43% | 8.218 | 2.35% | -3.218 |
| 19 | 3 | 0.86% | 7.797 | 2.23% | -4.797 |
| 20 | 4 | 1.14% | 7.416 | 2.12% | -3.416 |
| 21 | 6 | 1.71% | 7.071 | 2.02% | -1.071 |
| 22 | 6 | 1.71% | 6.757 | 1.93% | -0.757 |
| 23 | 7 | 2.00% | 6.469 | 1.85% | 0.531 |
| 24 | 7 | 2.00% | 6.205 | 1.77% | 0.795 |
| 25 | 7 | 2.00% | 5.962 | 1.70% | 1.038 |
| 26 | 4 | 1.14% | 5.737 | 1.64% | -1.737 |
| 27 | 3 | 0.86% | 5.528 | 1.58% | -2.528 |
| 28 | 5 | 1.43% | 5.334 | 1.52% | -0.334 |
| 29 | 3 | 0.86% | 5.153 | 1.47% | -2.153 |
| 30 | 2 | 0.57% | 4.984 | 1.42% | -2.984 |
| 31 | 1 | 0.29% | 4.826 | 1.38% | -3.826 |
| 32 | 3 | 0.86% | 4.677 | 1.34% | -1.677 |
| 33 | 4 | 1.14% | 4.538 | 1.30% | -0.538 |
| 34 | 5 | 1.43% | 4.406 | 1.26% | 0.594 |
| 35 | 2 | 0.57% | 4.282 | 1.22% | -2.282 |
| 36 | 0 | 0.00% | 4.165 | 1.19% | -4.165 |
| 37 | 3 | 0.86% | 4.054 | 1.16% | -1.054 |
| 38 | 3 | 0.86% | 3.948 | 1.13% | -0.948 |
| 39 | 4 | 1.14% | 3.848 | 1.10% | 0.152 |
| 40 | 6 | 1.71% | 3.753 | 1.07% | 2.247 |
| 41 | 4 | 1.14% | 3.663 | 1.05% | 0.337 |
| 42 | 2 | 0.57% | 3.577 | 1.02% | -1.577 |
| 43 | 2 | 0.57% | 3.494 | 1.00% | -1.494 |
| 44 | 6 | 1.71% | 3.416 | 0.98% | 2.584 |
| 45 | 2 | 0.57% | 3.341 | 0.96% | -1.341 |
| 46 | 4 | 1.14% | 3.269 | 0.93% | 0.731 |
| 47 | 1 | 0.29% | 3.2 | 0.91% | -2.2 |
| 48 | 4 | 1.14% | 3.134 | 0.90% | 0.866 |
| 49 | 5 | 1.43% | 3.071 | 0.88% | 1.929 |
| 50 | 5 | 1.43% | 3.01 | 0.86% | 1.99 |
| 51 | 3 | 0.86% | 2.952 | 0.84% | 0.048 |
| 52 | 1 | 0.29% | 2.895 | 0.83% | -1.895 |
| 53 | 2 | 0.57% | 2.841 | 0.81% | -0.841 |
| 54 | 4 | 1.14% | 2.789 | 0.80% | 1.211 |
| 55 | 1 | 0.29% | 2.739 | 0.78% | -1.739 |
| 56 | 3 | 0.86% | 2.69 | 0.77% | 0.31 |
| 57 | 4 | 1.14% | 2.644 | 0.76% | 1.356 |
| 58 | 3 | 0.86% | 2.598 | 0.74% | 0.402 |
| 59 | 3 | 0.86% | 2.555 | 0.73% | 0.445 |
| 60 | 3 | 0.86% | 2.513 | 0.72% | 0.487 |
| 61 | 2 | 0.57% | 2.472 | 0.71% | -0.472 |
| 62 | 2 | 0.57% | 2.432 | 0.70% | -0.432 |
| 63 | 1 | 0.29% | 2.394 | 0.68% | -1.394 |
| 64 | 1 | 0.29% | 2.357 | 0.67% | -1.357 |
| 65 | 6 | 1.71% | 2.321 | 0.66% | 3.679 |
| 66 | 1 | 0.29% | 2.286 | 0.65% | -1.286 |
| 67 | 2 | 0.57% | 2.252 | 0.64% | -0.252 |
| 68 | 0 | 0.00% | 2.219 | 0.63% | -2.219 |
| 69 | 5 | 1.43% | 2.187 | 0.63% | 2.813 |
| 70 | 5 | 1.43% | 2.156 | 0.62% | 2.844 |
| 71 | 3 | 0.86% | 2.126 | 0.61% | 0.874 |
| 72 | 2 | 0.57% | 2.097 | 0.60% | -0.097 |
| 73 | 2 | 0.57% | 2.068 | 0.59% | -0.068 |
| 74 | 4 | 1.14% | 2.04 | 0.58% | 1.96 |
| 75 | 4 | 1.14% | 2.013 | 0.58% | 1.987 |
| 76 | 2 | 0.57% | 1.987 | 0.57% | 0.013 |
| 77 | 2 | 0.57% | 1.961 | 0.56% | 0.039 |
| 78 | 3 | 0.86% | 1.936 | 0.55% | 1.064 |
| 79 | 1 | 0.29% | 1.912 | 0.55% | -0.912 |
| 80 | 1 | 0.29% | 1.888 | 0.54% | -0.888 |
| 81 | 3 | 0.86% | 1.865 | 0.53% | 1.135 |
| 82 | 2 | 0.57% | 1.842 | 0.53% | 0.158 |
| 83 | 7 | 2.00% | 1.82 | 0.52% | 5.18 |
| 84 | 3 | 0.86% | 1.799 | 0.51% | 1.201 |
| 85 | 1 | 0.29% | 1.778 | 0.51% | -0.778 |
| 86 | 4 | 1.14% | 1.757 | 0.50% | 2.243 |
| 87 | 3 | 0.86% | 1.737 | 0.50% | 1.263 |
| 88 | 2 | 0.57% | 1.718 | 0.49% | 0.282 |
| 89 | 3 | 0.86% | 1.698 | 0.49% | 1.302 |
| 90 | 1 | 0.29% | 1.68 | 0.48% | -0.68 |
| 91 | 2 | 0.57% | 1.661 | 0.48% | 0.339 |
| 92 | 2 | 0.57% | 1.643 | 0.47% | 0.357 |
| 93 | 5 | 1.43% | 1.626 | 0.46% | 3.374 |
| 94 | 1 | 0.29% | 1.609 | 0.46% | -0.609 |
| 95 | 1 | 0.29% | 1.592 | 0.46% | -0.592 |
| 96 | 2 | 0.57% | 1.575 | 0.45% | 0.425 |
| 97 | 0 | 0.00% | 1.559 | 0.45% | -1.559 |
| 98 | 2 | 0.57% | 1.543 | 0.44% | 0.457 |
| 99 | 1 | 0.29% | 1.528 | 0.44% | -0.528 |
Chi-Squared test, ᵪ2=95.493 p-value=0.299
Euclidean Distance Test, d=0.98899 p-value=0.484
Hotelling T-square test , Hotelling T2=25.377 p-value=0.659
Joenssen’s JP-square test, JP-square=0.6568 p-value=0.337
Kolmogorov-Smirnov (K-S) test, D=75.922 p-value=0.163
Chebyshev Distance (maximum norm) test, m=0.27686 p-value=0.847
Table 2: First two digits distribution the growth of confirmed case and tests of significance
Results
In every disease outbreak around the world, underreporting occurs; however, keeping track of the COVID-19 outbreak in developing countries has been particularly difficult. Understanding the national and global burden of COVID-19, as well as managing COVID-19 prevention and control efforts, requires an accurate count of national COVID-19 cases. Epidemiologists can predict a disease's trajectory, researchers can develop treatments and vaccines, responders can track transmission, and the public can protect itself with accurate reporting. Without public trust, full transparency is impossible, and authoritarian regimes have a persistent public trust deficit. To ensure the successful control of the epidemic and the prevention of secondary problems, COVID-19 outbreak management requires strong, transparent, and accountable leadership and communication strategies at all levels.
Conclusion
Benford's Law calculates the approximate frequency of digits in any numerical data and is commonly used to verify the accuracy of published data. It is especially applicable to a wide variety of financial data, and auditors often use it to detect fraud, misuse, or distortion of accounting data. In this study, Benford's Law was used to regulate COVID-19 results. Benford's Law, on the other hand, does not recommend a foolproof method of detecting fraud or manipulation; rather, it identifies problem areas that may be manipulated data.
We focus on measure the compliance of COVID-19 confirmed case data reported by Turkey with Benford’s Law. In light of increasing knowledge about applications of Benford’s laws, we have analysed distributions’ features of COVID-19 confirmed case over a long-time interval, that is, from March 2020, till the end of February 2021, amounting to 350 data points. We have addressed our considerations to the amount of the first, and first two significant digits. According to the different assessment approaches utilized for the first digits and first two digits, namely Chi-Squared test, Euclidean Distance test, Hotelling T-square test, Joenssen’s JP-square test, Kolmogorov-Smirnov (K-S) test, Chebyshev Distance test and Judge-Schechter Normed Deviation test, reported the confirmed case of COVID-19 data between 16 Mart 2020 to 28 February 2021 seemed to be almost in perfect conformity with Benford’s Law. According to all test results, the growth of confirmed case of COVID-19 seem to perfectly comply with Benford’s Law’s expected proportions, so we consider published data COVID-19 by Turkey is not fake.
References
- Lu R, Zhao X, Li J, Niu P, Yang B, Wu H, et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: Implications for virus origins and receptor binding. The lancet. 2020; 395(10224): 565-574.
[Crossref] [Google scholar] [Pubmed]
- World Health Organization. WHO Director-General’s remarks at the media briefing on 2019-nCoV on 11 February 2020.
- Ruan Q, Yang K, Wang W, Jiang L, Song J. Clinical predictors of mortality due to COVID-19 based on an analysis of data of 150 patients from Wuhan, China. Intensive Care Med. 2020; 46(5): 846-848.
[Crossref] [Google scholar] [Pubmed]
- World health organisation coronavirus disease (covid-19) dashboard. WHO. 2021.
- Turkey covid-19 patient table 17 June 2021. TR Ministry of Health. 2021.
- Benford F. The law of anomalous numbers. Proc Am Philos Soc. 1938: 551-572.
- Varian HR. Benfords law. American Statistician. 1972; 26(3): 65.
- Maximilano MZ, Fernado D, Fernado T. Tampering with inflation data: A Benford law-based analysis of national statistics in Argentina. Physica A: Statistical Mechanics and its Applications. 2019; 525: 761-770.
- Michalski T, Stoltz G. Do countries falsify economic data strategically? Some evidence that they might. Rev Econ Stat. 2013; 95(2): 591-616.
- Nye J, Moul C. The political economy of numbers: On the application of Benford's law to international macroeconomic statistics. The BE Journal of Macroeconomics. 2007; 7(1).
- Garcia GJ, Pastor G. Benford’s Law and Macroeconomic Data Quality, International Monetary Fund, 2009.
- Rauch B, Göttsche M, Brähler G, Kronfeld T. Deficit versus social statistics: Empirical evidence for the effectiveness of Benford’s law. Appl Econ Lett. 2014; 21(3): 147-151.
- Holz CA. The quality of China's GDP statistics. China Economic Review. 2014; 30: 309-338.
- Nigrini MJ. Persistent patterns in stock returns, stock volumes, and accounting data in the US capital markets. J Account Audit Finance. 2015; 30(4): 541-557.
- Barabesi L, Cerasa A, Cerioli A, Perrotta D. Goodness-of-fit testing for the Newcomb-Benford law with application to the detection of customs fraud. J Bus Econ Stat. 2018; 36(2): 346-358.
- Pericchi L, Torres D. Quick anomaly detection by the Newcomb-Benford Law, with applications to electoral processes data from the USA, Puerto Rico and Venezuela. Stat Sci. 2011: 502-516.
- Deckert J, Myagkov M, Ordeshook PC. Benford's Law and the detection of election fraud. Polit Anal. 2011; 19(3): 245-268.
- Alali FA, Romero S. Benford's Law: Analyzing a decade of financial data. J Emerg Technol Account. 2013; 10(1): 1-39.
- Grabiński K, Paszek Z. Examining re financial datase. ekonomske te ekonomske teme. 2013; 51(3): 515-524.
- Boyau JR, Bodin T, Scheffers A, Sambridge M, May SM. Using Benford’s law to investigate Natural Hazard dataset homogeneity. Scientific reports. 2015; 5(1): 1-8.
[Crossref] [Google scholar] [Pubmed]
- Pearson KFRS. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. London, Edinburgh Dublin Philos Mag J Sci. 1900; 50(302): 157-175.
- Kolmogorov A. Sulla determinazione empirica di una lgge di distribuzione. Inst Ital Attuari, Giorn. 1933; 4: 83-91.
- Drew JH, Glen AG, Leemis LM. Computing the cumulative distribution function of the Kolmogorov-Smirnov statistic. Comput Stat Data Anal. 2000; 34(1): 1-15.
- Cho WKT, Gaines BJ. Breaking the (Benford) law: Statistical fraud detection in campaign finance. Am Stat. 2007: 61(3): 218-223.
- Judge G, Schechter L. Detecting problems in survey data using Benford’s Law. J Hum Resour. 2009; 44(1): 1-24.
- Shapiro SS, Francia RS. An approximate analysis of variance test for normality. J Am Stat Assoc. 1972; 67(337): 215-216.
- Joenssen DW, Muellerleile T. Package ‘BenfordTests’. 2015.
Author Info
Hasraddin Guliyev*Citation: Guliyev H: COVID-19 Data Published by Turkey is Fake or Not?
Received: 15-Dec-2021 Accepted: 29-Dec-2021 Published: 05-Jan-2022, DOI: 10.31858/0975-8453.13.1.24-29
Copyright: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ARTICLE TOOLS
- Dental Development between Assisted Reproductive Therapy (Art) and Natural Conceived Children: A Comparative Pilot Study Norzaiti Mohd Kenali, Naimah Hasanah Mohd Fathil, Norbasyirah Bohari, Ahmad Faisal Ismail, Roszaman Ramli SRP. 2020; 11(1): 01-06 » doi: 10.5530/srp.2020.1.01
- Psychometric properties of the World Health Organization Quality of life instrument, short form: Validity in the Vietnamese healthcare context Trung Quang Vo*, Bao Tran Thuy Tran, Ngan Thuy Nguyen, Tram ThiHuyen Nguyen, Thuy Phan Chung Tran SRP. 2020; 11(1): 14-22 » doi: 10.5530/srp.2019.1.3
- A Review of Pharmacoeconomics: the key to “Healthcare for All” Hasamnis AA, Patil SS, Shaik Imam, Narendiran K SRP. 2019; 10(1): s40-s42 » doi: 10.5530/srp.2019.1s.21
- Deuterium Depleted Water as an Adjuvant in Treatment of Cancer Anton Syroeshkin, Olga Levitskaya, Elena Uspenskaya, Tatiana Pleteneva, Daria Romaykina, Daria Ermakova SRP. 2019; 10(1): 112-117 » doi: 10.5530/srp.2019.1.19
- Dental Development between Assisted Reproductive Therapy (Art) and Natural Conceived Children: A Comparative Pilot Study Norzaiti Mohd Kenali, Naimah Hasanah Mohd Fathil, Norbasyirah Bohari, Ahmad Faisal Ismail, Roszaman Ramli SRP. 2020; 11(1): 01-06 » doi: 10.5530/srp.2020.1.01
- Manilkara zapota (L.) Royen Fruit Peel: A Phytochemical and Pharmacological Review Karle Pravin P, Dhawale Shashikant C SRP. 2019; 10(1): 11-14 » doi: 0.5530/srp.2019.1.2
- Pharmacognostic and Phytopharmacological Overview on Bombax ceiba Pankaj Haribhau Chaudhary, Mukund Ganeshrao Tawar SRP. 2019; 10(1): 20-25 » doi: 10.5530/srp.2019.1.4
- A Review of Pharmacoeconomics: the key to “Healthcare for All” Hasamnis AA, Patil SS, Shaik Imam, Narendiran K SRP. 2019; 10(1): s40-s42 » doi: 10.5530/srp.2019.1s.21
- A Prospective Review on Phyto-Pharmacological Aspects of Andrographis paniculata Govindraj Akilandeswari, Arumugam Vijaya Anand, Palanisamy Sampathkumar, Puthamohan Vinayaga Moorthi, Basavaraju Preethi SRP. 2019; 10(1): 15-19 » doi: 10.5530/srp.2019.1.3